The Newcomb-Benford Law
Simon Newcomb (12 Mar 1835 – 11 July 1909), a self-taught Canadian-American mathematical astronomer, was a man of many diverse accomplishments (though a rather unpleasant individual in some ways) but nowadays principally remembered for noticing (at some point in 1881) that the later pages of his university library copy of the logarithm tables were progressively less well-thumbed than the earlier ones.
The tabulation was evidently to a good many significant figures, requiring a good many pages, of course.
The pages at the beginning of the book, for those numbers starting with a 1, were the most worn, while the pages at the end of the book, for those numbers starting with a 9, were the least worn. The pages in between, for intermediate numbers starting with digits between 2 and 8, were of steadily decreasing dilapidation.
What could account for this, he wondered?
We have to be rather cautious at this point...
Logarithms are typically displayed for the numbers (to so many significant figures) between zero and unity and are purely mathematical in origin. They are not at issue, and aren’t subject to the Benford effect. If you don’t believe me, please see the Frank Castle four-figure log table.
Though it was logarithms that had caught his eye, it was the table of antilogarithms, which represented the real-world data that the logarithms had processed, that were indeed subject to the effect. Please see the corresponding Frank Castle four-figure antilog table for visual confirmation and (further down) a tabulation of my own tally.

Please click here for the log table, here for the antilog table,
and here for the nitty-gritty of using them (no gain without pain).
Indeed, he devised an inspired formula to quantify the relative frequencies of the initial digits of the numbers in the antilogarithm table. It gave the probability of a real-world number beginning with the digit d as being log (d + 1) – log (d).
This can be graphically displayed as per the ‘borrowed’ barchart below
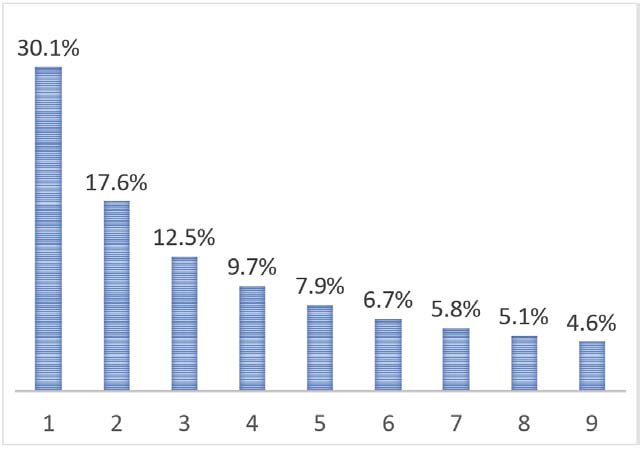
As also by the next such, in which Frank Benford’s hijacking of the idea in 1938 is clearly evident.
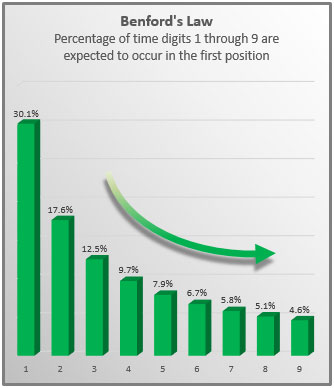
Stigler’s law of eponomy is validated once again!
Perhaps of interest is my own tally of the digits as per the Frank Castle antilog table:
| d | Count | % |
| 1 | 301 | 30.1 |
| 2 | 177 | 17.7 |
| 3 | 125 | 12.5 |
| 4 | 96 | 9.6 |
| 5 | 80 | 8.0 |
| 6 | 67 | 6.7 |
| 7 | 58 | 5.8 |
| 8 | 51 | 5.1 |
| 9 | 45 | 4.5 |
| Total | 1,000 | 100.0 |
(I've repeated this exercise using the Frank Castle 5 figure antilog table and the only difference is that 301->302 and 177->176)
Newcomb was a busy man, and this was just an interesting oddity, so after dashing off a note to The American Journal of Mathematics, he probably forgot all about it.

Frank Benford
But waiting round the corner with a sockful of sand (as P G Wodehouse would have put it) was the Efficient Baxter as personified by Frank Benford, whose tireless researches into countless numerical tabulations of almost every aspect of humanly recorded data have corroborated Newcomb’s formula (subject to certain T & C’s, of course).
Benford seems to have quoted Newcomb’s formula as his own (calling it the “The Law of Anomalous Numbers” in his publication Proc Am Phil Soc vol 78 (1938) p551, and saying that the law “evidently goes deeper among the roots of primal causes than our number system unaided can explain”) but made no effort to justify it theoretically. And neither shall I, as statistics are my Achilles heel.
But, nevertheless, I’d like to put it under the microscope briefly. Another way to express the formula is simply log (d + 1) – log (d) = log (1 + 1/d), and as tabulated below.
| d | 1 + 1/d | decimal | log (4 sf) | % |
| 1 | 2 | 2.0 | 0.3010 | 30.10 |
| 2 | 3/2 | 1.5 | 0.1761 | 17.61 |
| 3 | 4/3 | 1.333 | 0.1249 | 12.49 |
| 4 | 5/4 | 1.25 | 0.0969 | 9.69 |
| 5 | 6/5 | 1.2 | 0.0792 | 7.92 |
| 6 | 7/6 | 1.167 | 0.0661 | 6.71 |
| 7 | 8/7 | 1.143 | 0.0581 | 5.81 |
| 8 | 9/8 | 1.125 | 0.0511 | 5.11 |
| 9 | 10/9 | 1.111 | 0.0457 | 4.57 |
| Total | 1 | 100.0 |
log(2) +
log(3/2) + log(4/3) + log(5/4) + log(6/5) + log(7/6) + log(8/7) + log(9/8) + log(10/4)
= log{2 x (3/2) x (4/3) x (5/4) x (6/5) x (7/6) x (8/7) x (9/8) x (10/4)}
= log(10) = 1
which is rather neat.
Dropping down to one place of decimals it's also neat to note that
| d | % | Combinations |
| 1 | 30.1 | |
| 2 | 17.6 | 17.6 + 12.5 = 30.1 |
| 3 | 12.5 | |
| 4 | 9.7 | 9.7 + 7.9 = 17.6 |
| 5 | 7.9 | |
| 6 | 6.7 | 6.7 + 5.8 = 12.5 |
| 7 | 5.8 | |
| 8 | 5.1 | 5.1 + 4.6 = 9.7 |
| 9 | 4.6 |
It is said that the law (or perhaps one should say tendency) is invariant to change of logarithmic base (whether binary or decimal or duodecimal, for example) and is also independent of the units of measurement (whether, for example, gallons per mile or litres per kilometre). In fact, it’s an inexhaustible topic for mathematical mining for generations to come.
It has also been very effectively weaponised in the investigation of bogus financial data, as best described (along with much else relating to its fundamentals) by Alex Bellos in chapter 2 of “Alex through the looking glass”, Bloomsbury 2015.


